Математик из Москвы решил «задачу о дощечках», которую разгадывали 40 лет
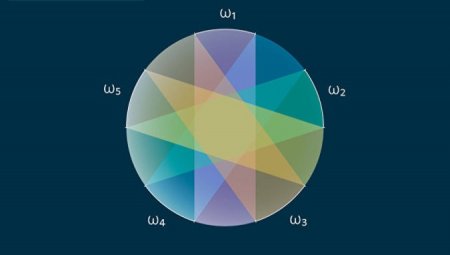
Российский преподаватель из Московского физико-технического института вместо со своим коллегой из Израиля решили «теорему о дощечках», над которой уже 40 лет ломают голову математики. Суть задачи в том, что круг можно полностью покрыть полосками, чья совокупная ширина не превышает его длину. Простыми словами, круг любых размеров невозможно покрыть дощечками, чья общая ширина меньше диаметра самой окружности. У этой задачи оказалось изящное решение, и нам посчастливилось его найти. Она навела нас на мысль о другой, более сильной гипотезе о покрытии сферы смещёнными зонами, полученными пересечением единичной сферы с трёхмерными полосками-дощечками, не обязательно симметричными относительно центра, рассказывает Александр Полянский, математик из Московского физтеха в Долгопрудном.
Решение этой задачи поможет разобраться в других спорных моментах дискретной геометрии, считает математик. Например, какое наибольшее число шаров одинакового размера можно разместить вокруг одного такого же шара. Такие теоремы интересны и с практической точки зрения, так как они напрямую связаны со многими проблемами в IT, физике и химии, сообщает РИА Новости. «Теорема о дощечках» была сформулирована еще в начале прошлого столетия, и около 50 лет назад математики Альфред Тарский и Трегер Бангом предложили простые варианты ее решения. Через несколько лет, в 1973 году венгерский математик Лазл Фейеш Тот выдвинул более сложную версию «теоремы о дощечках»: сферическую поверхность любых размеров можно покрыть произвольным набором трехмерных «дощечек», чья общая толщина не превысит длину окружности. Ответ на сложную задачку последовал только через 40 лет, когда Полянский его коллега Цзылинь Цзян смогли не только решить задачу Лазла Тота, но и показать, что она будет работать и в многомерном пространстве, опираясь на идеи, которые использовал Трегер Банг для того, чтобы доказать первую многомерную версию «теоремы о дощечках». Математики предположили, что суммарная ширина «дощечек», полностью покрывающих сферу, будет меньше длины окружности, для этого им нужно было бы противоречие в виде точки, которая лежала бы на сфере, но не была покрыта зонами. В итоге ученые смогли найти такое противоречие, что доказало теорему, выдвинутую в 1973 году.
Вернуться назад